三角函数

函数定义

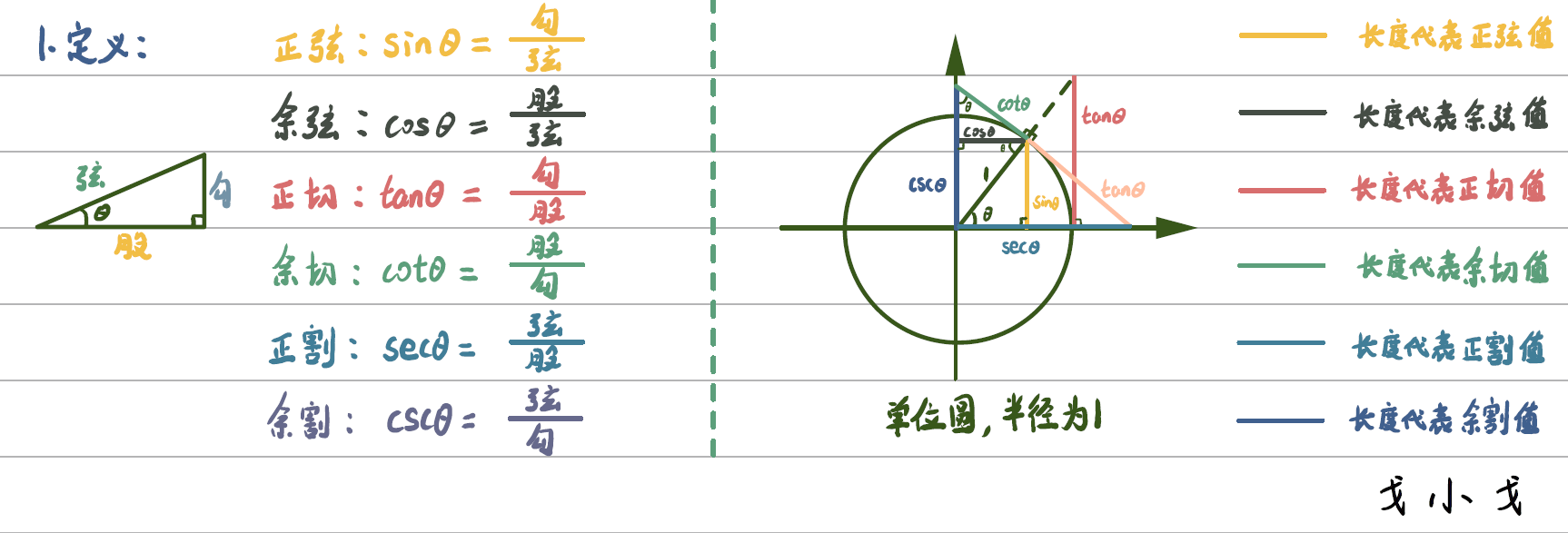
函数图像

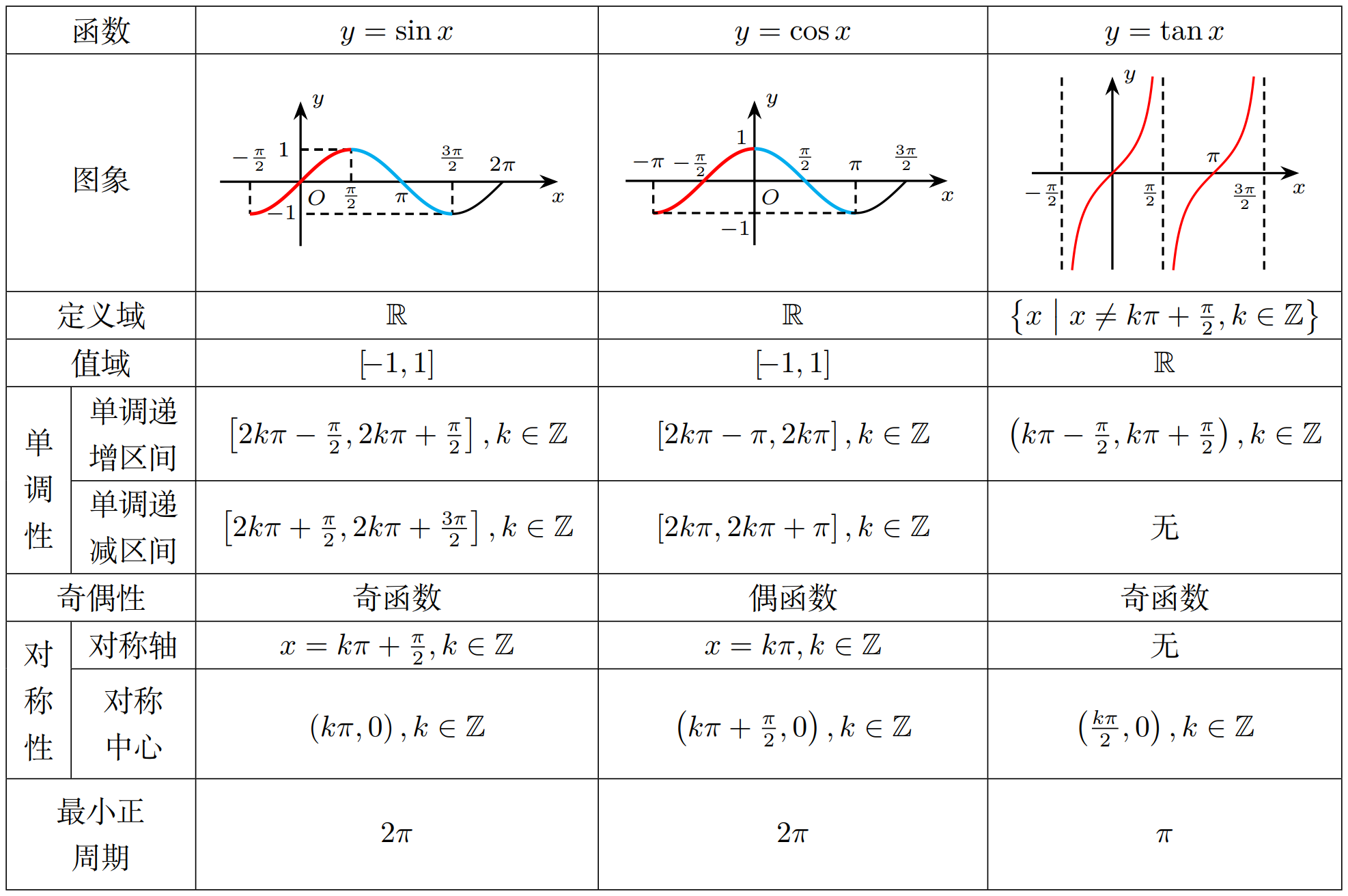
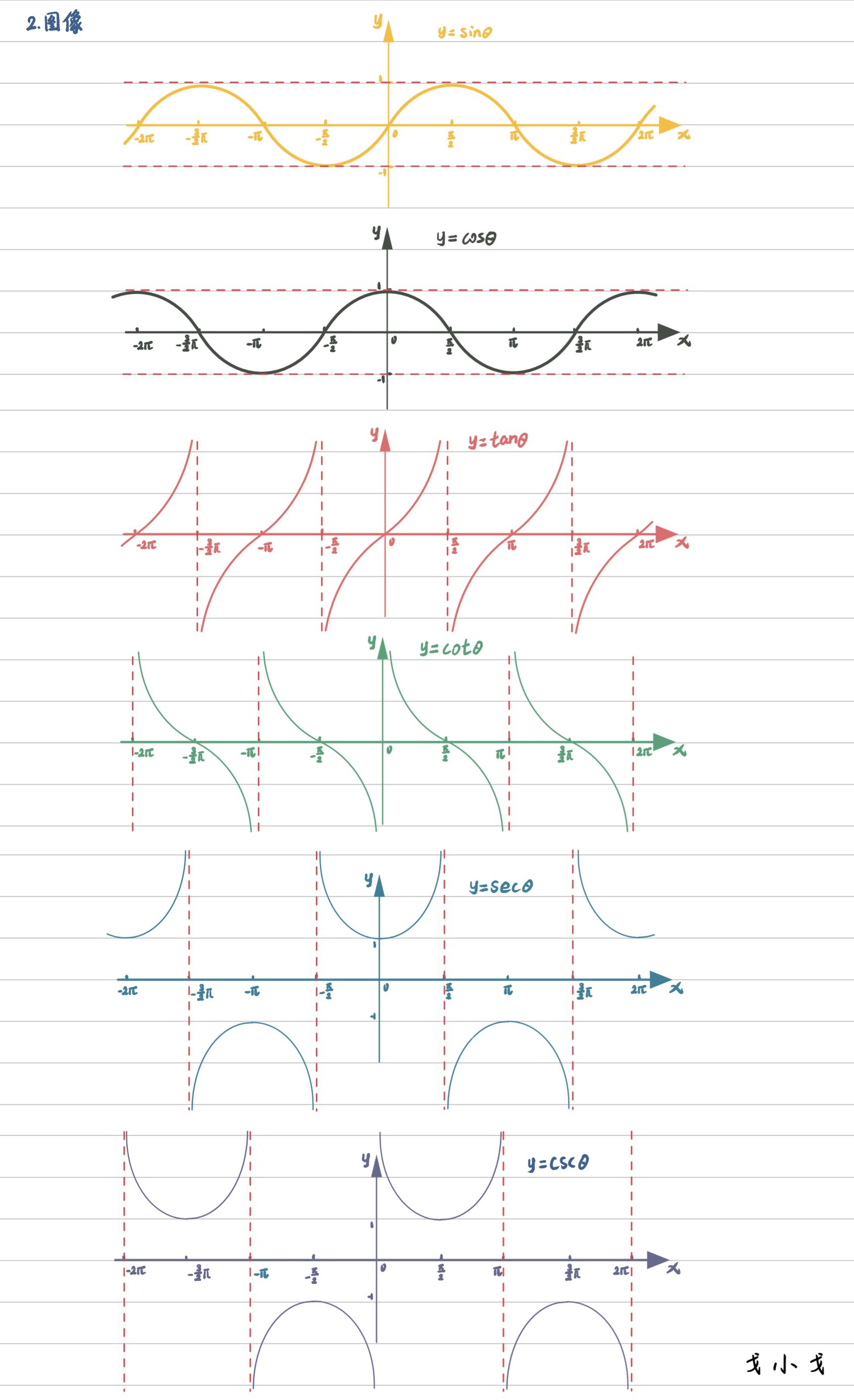
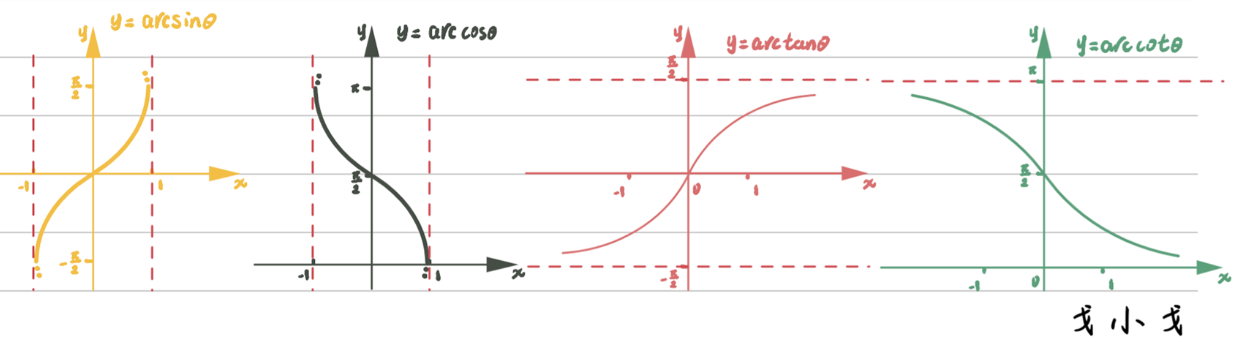
函数关系

• $tanα = \dfrac{sinα}{cosα}$

• $sin^{2}α + cos^{2}α = 1$

---

• $1 + sin2α = (sinα + cosα)^{2}$

• $1 - sin2α = (sinα - cosα)^{2}$

---

更多关系请参考如下六边形记忆图

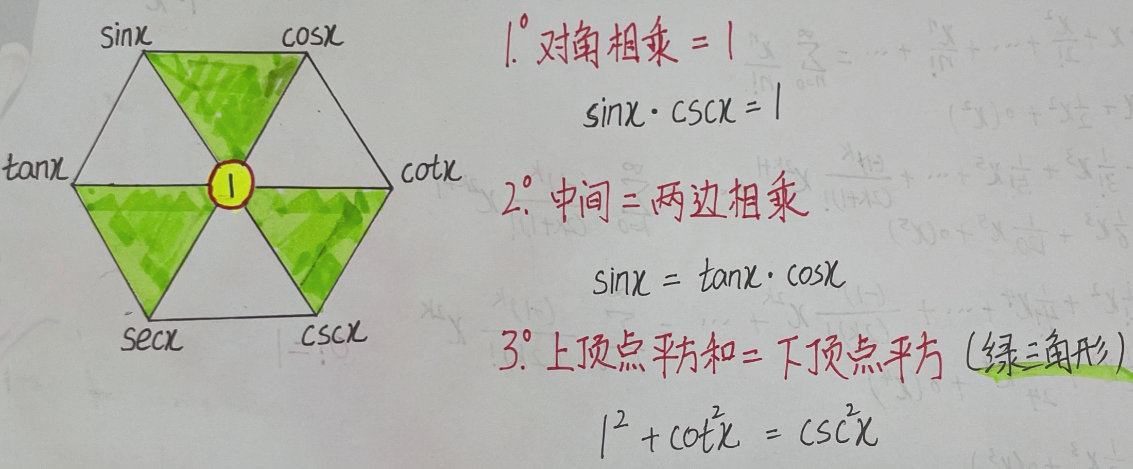
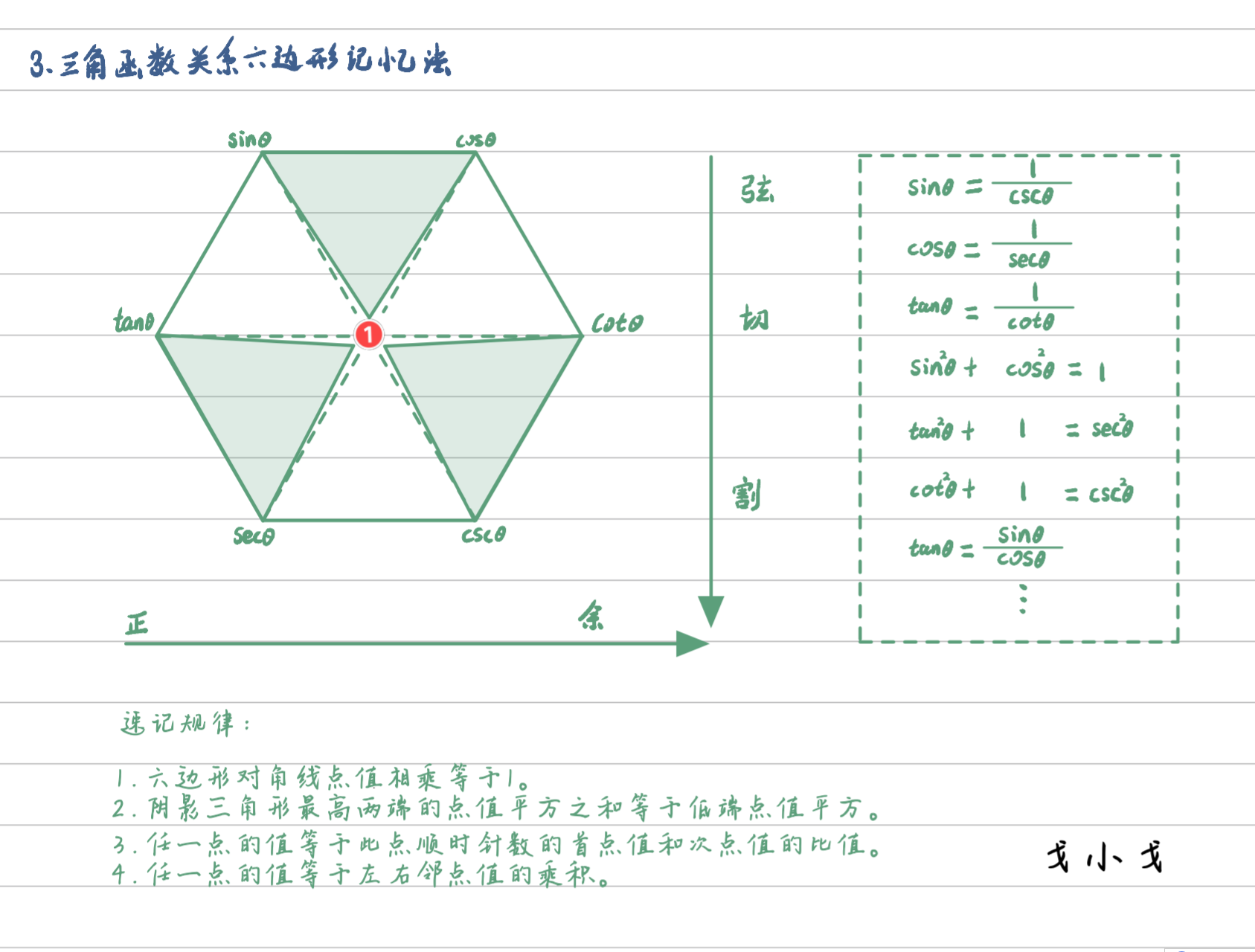
函数特殊值

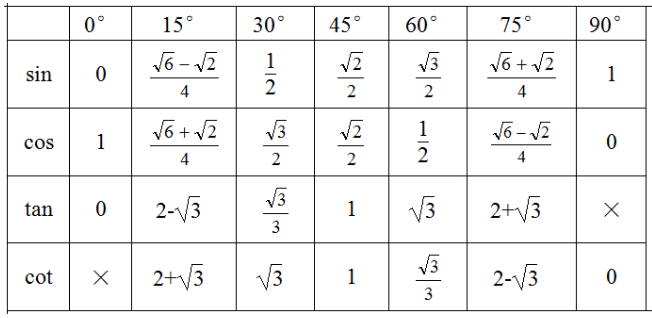
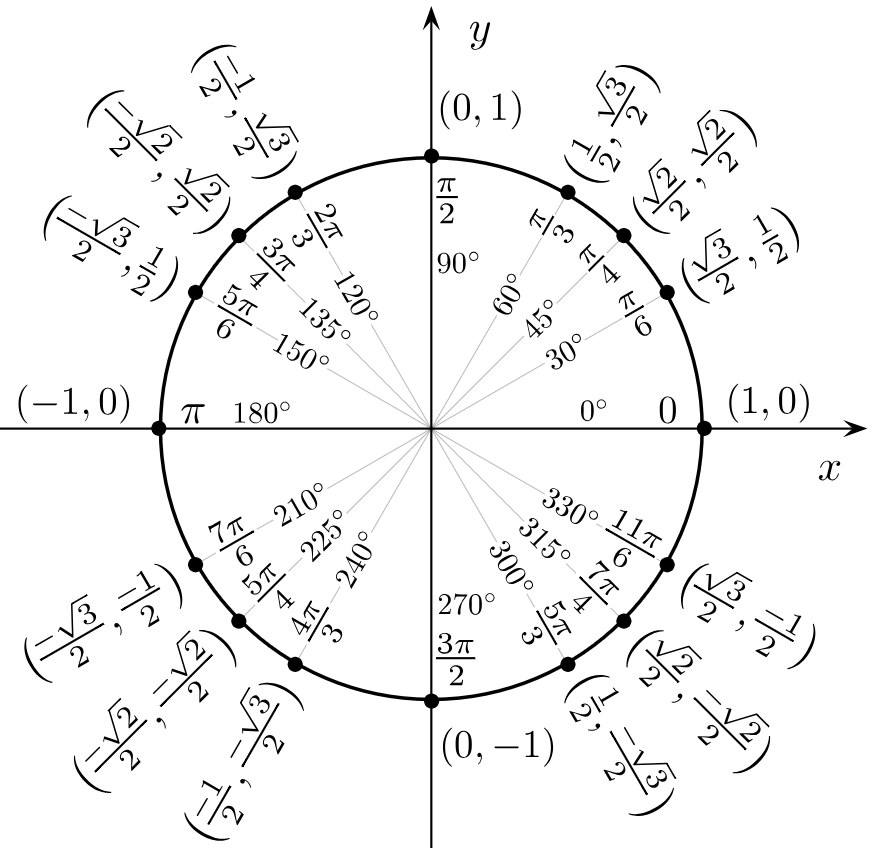
边角关系

正弦定理

$\dfrac{a}{sinA} = \dfrac{b}{sinB} = \dfrac{c}{sinC} = 2R$

余弦定理

• $a^{2} = b^{2} + c^{2} - 2bccosA$
• $b^{2} = a^{2} + c^{2} - 2accosB$
• $c^{2} = a^{2} + b^{2} - 2abcosC$

---

• $cosA = \dfrac{b^{2} + c^{2} - a^{2}}{2bc}$

• $cosB = \dfrac{a^{2} + c^{2} - b^{2}}{2ac}$

• $cosC = \dfrac{a^{2} + b^{2} - c^{2}}{2ab}$

基本公式

诱导公式

• $sin(2kπ + α) = sinα，k∈Z$
• $cos(2kπ + α) = cosα，k∈Z$
• $tan(2kπ + α) = tanα，k∈Z$

---

• $sin(-α) = -sinα$
• $cos(-α) = cosα$
• $tan(-α) = -tanα$

---

• $sin(π + α) = -sinα$
• $cos(π + α) = -cosα$
• $tan(π + α) = tanα$

---

• $sin(π - α) = sinα$
• $cos(π - α) = -cosα$
• $tan(π - α) = -tanα$

---

• $sin(\dfrac{π}{2} + α) = cosα$

• $cos(\dfrac{π}{2} + α) = -sinα$

• $tan(\dfrac{π}{2} + α) = -cotα$

• $sin(\dfrac{π}{2} - α) = cosα$

• $cos(\dfrac{π}{2} - α) = sinα$

• $tan(\dfrac{π}{2} - α) = cotα$

TIP

奇变偶不变，符号看象限。
可参考：三角函数公式解析

和差角公式

• $sin(α + β) = sinαcosβ + cosαsinβ$
• $sin(α - β) = sinαcosβ - cosαsinβ$
• $cos(α + β) = cosαcosβ - sinαsinβ$
• $cos(α - β) = cosαcosβ + sinαsinβ$

---

• $tan(α + β) = \dfrac{tanα + tanβ}{1 - tanαtanβ}$

• $tan(α - β) = \dfrac{tanα - tanβ}{1 + tanαtanβ}$

倍角公式

• $sin2α = 2sinαcosα$

• $cos2α = cos^{2}α - sin^{2}α = 1 - 2sin^{2}α = 2cos^{2}α - 1$

• $tan2α = \dfrac{2tanα}{1 - tan^{2}α}$

半角公式

• $sin\dfrac{α}{2} = \pm \sqrt{\dfrac{1 - cosα}{2}}$

• $cos\dfrac{α}{2} = \pm \sqrt{\dfrac{1 + cosα}{2}}$

• $tan\dfrac{α}{2} = \pm \sqrt{\dfrac{1 - cosα}{1 + cosα}} = \dfrac{sinα}{1 + cosα} = \dfrac{1 - cosα}{sinα}$

降幂公式

• $sin^{2}α = \dfrac{1 - cos2α}{2}$

• $cos^{2}α = \dfrac{1 + cos2α}{2}$

• $tan^{2}α = \dfrac{1 - cos2α}{1 + cos2α}$

和差化积公式

• $sinα + sinβ = 2sin\dfrac{α + β}{2}cos\dfrac{α - β}{2}$

• $sinα - sinβ = 2cos\dfrac{α + β}{2}sin\dfrac{α - β}{2}$

• $cosα + cosβ = 2cos\dfrac{α + β}{2}cos\dfrac{α - β}{2}$

• $cosα - cosβ = -2sin\dfrac{α + β}{2}sin\dfrac{α - β}{2}$

• $tanα + tanβ = \dfrac{sin(α + β)}{cosαcosβ}$

积化和差公式

• $sinαcosβ = \dfrac{1}{2}[sin(α + β) + sin(α - β)]$

• $cosαsinβ = \dfrac{1}{2}[sin(α + β) - sin(α - β)]$

• $sinαsinβ = \dfrac{1}{2}[cos(α - β) - cos(α + β)]$

• $cosαcosβ = \dfrac{1}{2}[cos(α - β) + cos(α + β)]$

万能公式

• $sinα = \dfrac{2tan\dfrac{α}{2}}{1 + tan^{2}\dfrac{α}{2}}$

• $cosα = \dfrac{1 - tan^{2}\dfrac{α}{2}}{1 + tan^{2}\dfrac{α}{2}}$

• $tanα = \dfrac{2tan\dfrac{α}{2}}{1 - tan^{2}\dfrac{α}{2}}$

辅助角公式